Cách bấm máy tính Lim - Giới hạn hàm số

Tính số lượng giới hạn Lim đưa đi ra cách thức và những ví dụ rõ ràng, hùn chúng ta học viên trung học phổ thông ôn tập dượt và gia tăng kiến thức và kỹ năng về dạng toán tính số lượng giới hạn 11 và lớp 12. Tài liệu bao gồm cách bấm PC số lượng giới hạn những bài bác tập dượt ví dụ minh họa sở hữu tiếng giải và bài bác tập dượt tập luyện hùn chúng ta khái quát nhiều dạng khác nhau bài bác chuyên mục số lượng giới hạn hàm số. Chúc chúng ta học hành hiệu quả!

A. Giới hạn dung lượng giác

B. Giới hạn hàm siêu việt

C. Cách tính lim sử dụng máy tính

Bước 1: Nhập hàm số

Bạn đang xem: Cách bấm máy tính Lim - Giới hạn hàm số

Bước 2: Sử dụng hàm CALC nhằm tính giới hạn

Quy dự trù số lượng giới hạn vô toan như sau:

$\begin{matrix} x \to + \infty \Rightarrow x = {10^9} \hfill \\ x \to - \infty \Rightarrow x = {10^{ - 9}} \hfill \\ x \to {x_0}^ + \Rightarrow x = {x_0} + {10^{ - 6}} \hfill \\ x \to {x_0}^ - \Rightarrow x = {x_0} - {10^{ - 6}} \hfill \\ x \to {x_0} \Rightarrow x = {x_0} + {10^{ - 6}} \hfill \\ \end{matrix}$

Chú ý: Vì đấy là mẹo nhỏ nhằm tính số lượng giới hạn nên thành quả PC thể hiện chỉ sấp xỉ đáp án, nên tao tiếp tục lựa chọn đáp án sớm nhất.

D. Tính lim sử dụng máy tính

Ví dụ 1: Tính số lượng giới hạn của hàm số $\frac{{{e^{2x}} - 1}}{{\sqrt {x + 4} - 2}}$ Khi x tiến thủ cho tới 0.

Hướng dẫn giải

Quan sát hàm số tao sở hữu $x \to 0 \Rightarrow x = 0 + {10^{ - 6}}$

Sử dụng PC Casio nhằm tính số lượng giới hạn như sau:

Bước 1: Nhập hàm số vô PC tao được:

Cách bấm PC lim

Bước 2: Nhấn phím CALC ➟ 0 + 10^(-6) ➟ Nhấn lốt “=” tao được

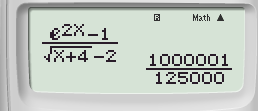
Cách bấm PC lim

Bước 3: Nhấn phím ta được kết quả:

Kết ngược sớm nhất là 8

Vậy lựa chọn đáp án B

Ví dụ 2: Tính $\lim \frac{{{n^3} + 4n - 5}}{{3{n^3} + {n^2} + 7}}$

Hướng dẫn giải

Quan sát hàm số tao thấy đề bài bác ko nói đến độ quý hiếm n tiến thủ cho tới từng nào thì tao tiếp tục hiểu rằng $n \to + \infty \Rightarrow n = {10^9}$

Sử dụng PC Casio nhằm tính số lượng giới hạn như sau:

Bước 1: Nhập hàm số vô PC tao được:

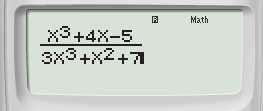
Cách bấm PC lim

Bước 2: Nhấn phím CALC ➟ 10^(9) ➟ Nhấn lốt “=” tao được

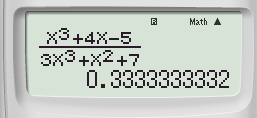
Cách bấm PC lim

Kết ngược sớm nhất là $\frac{1}{3}$

Vậy lựa chọn đáp án A

Ví dụ 3: Giới hạn $\lim \frac{{2 - {5^{n + 2}}}}{{{3^n} + {{2.5}^n}}}$ bởi vì bao nhiêu?

A. $\frac{{ - 25}}{2}$

Xem thêm: Cách khắc phục iPhone 13 Pro Max bị xanh, trắng màn hình cực hiệu quả

B. $\frac{{15}}{2}$

C. 0

D. -1

Hướng dẫn giải

Quan sát hàm số tao thấy đề bài bác ko nói đến độ quý hiếm n tiến thủ cho tới từng nào thì tao tiếp tục hiểu rằng $n \to + \infty \Rightarrow n = {10^9}$

Tuy nhiên xem xét, bài bác này tương quan đ ến hàm lũy quá (số mũ) nhưng mà PC chỉ tính được số nón tối nhiều là 100 nên tao lựa chọn x = 100

Sử dụng PC Casio nhằm tính số lượng giới hạn như sau:

Bước 1: Nhập hàm số vô PC tao được:

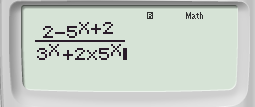
Cách bấm PC lim

Bước 2: Nhấn phím CALC ➟ 100 ➟ Nhấn lốt “=” tao được

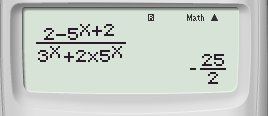
Cách bấm PC lim

Vậy lựa chọn đáp án A

Ví dụ 4: Tính số lượng giới hạn $\lim \left[ {1 + \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{n\left( {n + 1} \right)}}} \right]$

Hướng dẫn giải

Đối với sản phẩm số như vậy này tất cả chúng ta ko thể nhập vô PC cả biểu thức được

Bước 1: Tiến hành rút gọn gàng biểu thức như sau:

$\begin{matrix} 1 + \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{n\left( {n + 1} \right)}} \hfill \\ = 1 + \dfrac{{2 - 1}}{{1.2}} + \dfrac{{3 - 2}}{{2.3}} + \dfrac{{4 - 3}}{{3.4}} + ... + \dfrac{{n + 1 - n}}{{n\left( {n + 1} \right)}} \hfill \\ = 1 + \dfrac{1}{1} - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{n} - \dfrac{1}{{n + 1}} \hfill \\ = 2 - \dfrac{1}{{n + 1}} \hfill \\ \end{matrix}$

Sau Khi rút gọn gàng đi ra tiến hành bấm PC tương tự động những ví dụ bên trên.

Quan sát hàm số tao thấy đề bài bác ko nói đến độ quý hiếm n tiến thủ cho tới từng nào thì tao tiếp tục hiểu rằng $n \to + \infty \Rightarrow n = {10^9}$

Sử dụng PC Casio nhằm tính số lượng giới hạn như sau:

Bước 2: Nhập hàm số vô PC tao được:

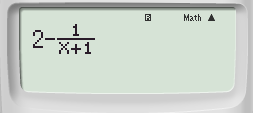
Cách bấm PC lim

Bước 3: Nhấn phím CALC ➟ 1➟ Nhấn lốt “=” tao được

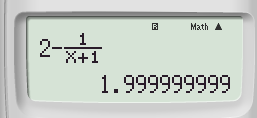
Cách bấm PC lim

Kết ngược cảm nhận được ngay gần 2 nhất

Xem thêm:

Chọn đáp án D

-----------------------------------------------------------

Hi vọng Chuyên đề Giới hạn của hàm số là tư liệu hữu ích mang đến chúng ta ôn tập dượt đánh giá năng lượng, hỗ trợ mang đến quy trình học hành vô lịch trình trung học phổ thông tương đương ôn luyện mang đến kì ganh đua trung học phổ thông Quốc gia. Chúc chúng ta học tập tốt!